몰아서 한 넘에게 독박을 씌우는게 깨달음이다. 전체를 한 줄에 꿰어 통짜덩어리로 상대해준다. 자연계의 모든 운동은 전자기력으로 설명된다. 수학의 모든 영역은 집합론으로 설명된다. 구조론의 상호작용으로 모두 설명한다.
집합론을 창시한 칸토어는 반대파에게 괴롭힘을 당해 정신병원에서 생을 마감해야 했다. 필자가 구조론 전파에 애를 먹듯이 칸토어도 고생 깨나 했다. 남보다 먼저 알면 괴롭다. 이때 사실이 아니라 언어의 문제로 고통받는다.
칸토어는 수(數)라는 단어의 개념을 바꾸었다. 상식을 뒤집었다. 이는 룰에 관한 문제이므로 국회에서 입법을 하듯이 학자들이 회의를 해서 결정해야 한다. 혼자 독단적으로 국어사전을 바꾸려들면 당연히 말썽이 나는 것이다.
멀쩡한 이태리가구를 필자가 ‘가구가 아니다’고 선언하는 격이다. 어쨌든 인상주의 화가들은 낡은 그림을 밀어내서 그것을 더 이상 그림이 아니게 만들어 버렸다. 사회의 룰이 바뀌었다. 구조론도 관점을 바꾸고 룰을 바꾼다.
아인슈타인도 그렇다. 시공간이 휘어진다는 사실이 문제가 아니라 관측결과를 그런 식으로 표현해도 되느냐는 언어의 문제에 부딪힌다. 시공간의 절대성을 전제로 하는 기존체계 안에서 설명방법을 찾는 노력을 왜 않느냐다.
“야임마! 기존의 뉴턴체계 안에서도 얼마든지 설명할 방법이 있을건데 노력해보지도 않고 왜 그래? 깽판놓자는 거야? 네가 물리학자 맞아?”
언어를 바꾸는 문제는 만인이 합의해야 한다. 그러려면 만인이 지켜보는 쇼를 베풀어야 한다. 아인슈타인은 일식쇼로 언론을 타서 그 문제를 해소했다. 전 세계인이 쇼를 지켜봤기 때문에 저절로 언어의 문제가 해소되었다.
김기덕 감독은 황금사자상 수상으로 그 문제를 돌파했다. 전 국민이 지켜보는 앞에서 거창한 이벤트를 벌여 더 이상의 불필요한 논쟁을 종식시킨 것이다. 그러나 칸토어는 끝까지 핍박받았다. 아래는 위키백과 발췌인용이다.

독일의 수학자 게오르크 칸토어(Georg Cantor)는 수학 기초론의 바탕이 된 집합론으로 잘 알려져 있다. 그는 집합간의 일대일 대응의 중요성을 확립하고 무한과 정렬된 집합을 정의하였으며, 자연수보다 실수가 “훨씬 많음”을 증명하였다.
초한수에 관한 칸토어의 이론이 일상적인 직관과 너무나 상치되는 충격적인 개념이어서 크로네커, 푸앵카레 등 동시대 수학자들은 그의 이론을 거부하였다. (중략) 1897년까지 그는 기초 집합론에서 몇 가지 역설을 발견했다. 말년에는 제1차 세계대전 시기와 겹쳐 가난하고 굶주리며 살다가, 결국 독일의 할레에서 정신병에 걸린 채 사망하였다.
칸토어의 혁신적인 수학은 그의 전 생애에 걸쳐 크로네커 등의 거센 반대에 부딪혔다. 현대의 대다수 수학자들은 그의 초한수에 대한 결과를 받아들이고서 그 위에 수학을 확립하였으며, 이는 중요한 수학적 방법론의 패러다임의 변화로 여겨지기도 한다.
칸토어의 ‘일대일 대응’ 개념은 구조론과 유사하다. 구조론은 크기를 배제한다. 크기를 배제한다는 것은 숫자가 0,1,2,3…의 자연수임을 부정한다는 것이다. 구조론에 자연수는 없다. 자연수는 자의 눈금이기 때문이다.
구조론은 눈금 지우고 시작한다. 눈금 지우면? 콤파스로 돌아간다. 자는 콤파스의 다리를 부러뜨린 것이다. 자의 수학이냐 콤파스의 수학이냐? 역시 언어의 문제다. 자의 수학과 콤파스의 수학은 자베르와 장발장처럼 절대로 공존할 수 없다. 하나는 반드시 꺾여야 한다.
◎ 자의 수학 - ●는 1이다.
◎ 콤파스의 수학 - ●와 ●의 사이에서 연결하는 링크가 1이다.
구조론은 콤파스를 쓰므로 눈금이 없다. 무엇인가? 구조론의 점, 선, 각, 입자, 밀도는 크기가 없다. 선(線)이라면 ‘긴 선’을 생각하지만 구조론의 선은 길이가 없다. 면(面)이라면 넓은 면을 생각하지만 구조론의 각(角)은 너비가 없다. 구조론의 입체는 체적이 없다. 콤파스는 원래 그게 없다.
무엇인가? 칸토어의 일대일 대응이다. 구조론은 마이너스이므로 밀도로부터 시작한다. 밀도 입체 각 선 점의 순서다. 그러나 밀도는 집합이고 숫자는 원소이므로 원소부터 시작하면 점에서 시작된다.
점은 크기가 없다. 우주의 허공에 한 점을 찍어보자. 거기다가 하나의 점을 추가하자. 점 둘이 잇닿으면 선이 된다. ●●다. 그러나 구조론의 점과 선은 크기가 없으므로 ●●는 인정되지 않는다. 무한히 작은 점을 찍어야 한다.
크기가 있는 점 ●에다 점 ●를 더하면 선이 되는게 아니라 두 점이 된다. 점 점=선이라는 생각은 이미 크기를 부여한 관념이다. 자가 아니라 콤파스여야 한다. 크기를 배제하라. 그렇다면 선은 불성립이다. 점 점=두 점이다.
점에서 선으로 비약하려면? 구조론의 1은 A나 B가 아니라 A와 B 사이에 연결하는 링크다. 당구공 둘이 충돌한다면 그 접점은 하나의 점이며 그 점은 크기가 없다. 두 당구공 사이에 하나의 링크가 있으며 1이다.
○○다. 여러분은 두 당구공들 사이에 하나의 점이 성립함을 알수 있다. 여기에 하나의 점을 추가해 보자. 가능한가? ○A○B○로 하면 점 A와 점B가 생긴다. 그러나 이 경우는 점들이다. 선이 아니라 점 2인 것이다. 실패다.
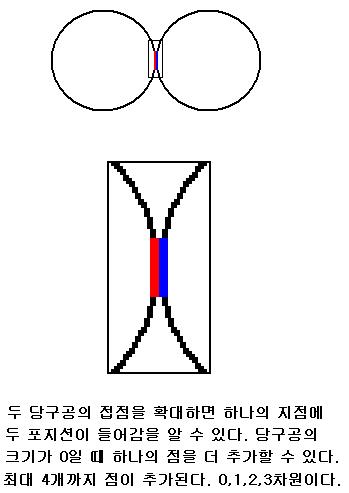
선이 되려면 어떻게 해야 할까? 두 당구공 중의 하나를 굴려야 한다. 굴리면 당구공 표면에 선이 그어진다. 그 굴리는 길이가 0이면 이렇게 된다.
평면 상에 그림으로 나타낼 수는 없지만 당구공의 크기가 0이라고 볼 때 최대 네 개의 포지션이 이런 식으로 집적된다. 각 0, 1, 2, 3차원을 이룬다. 여기에 운동 혹은 시간을 추가하면 4차원 밀도가 탄생한다.
자연에서 하나의 지점에 인접할 수 있는 포지션의 최대 숫자는 자기를 포함해서 5다. 그것이 구조론이다. 단 다섯 번째는 하나가 들어올 때 동시에 하나가 나가야만 한다. 교대순간에 5를 성립시킬 뿐 그 상태가 유지되지 않는다.
가속도처럼 에너지가 계속 들어올 때는 그 상태가 유지되지 않으면서도 유지되는 효과를 낸다. 그것이 4차원의 세계다. 4차원은 가속운동을 할 때만 있다. 에너지의 투입없이, 어떤 운동이나 변화의 새로운 촉발이 없이 그 상태가 유지되는 관성계 안에서는 3차원 밖에 없다.
폭발이나 변화, 운동의 촉발은 4차원을 이룬다. 지속적인 폭발은 4차원을 유지한다. 그러므로 4차원의 세계를 보는 것도 어렵지 않다. 계에 밀도가 걸려 운동하고 있는, 작동하고 있는 것이 4차원이다.
4차원 밀도는 3차원 공간에 에너지(시간)가 투입되어 질량을 형성한 것이며 3차원은 거기서 에너지를 뺀 멈춘 공간이다. 우주는 팽창하고 있기 때문에 실제로는 4차원이다. 다만 관측영역은 대개 3차원이다.
손으로 컵을 쥔다면 어떨까? 손의 에너지는 컵뿐만 아니라 컵을 받치고 있는 탁자에도 전달된다. 중력에 의한 마찰력 때문에 컵과 컵이 아닌 부분의 구분은 명확하지 않다. 실상 컵이라는 것도 전자기력에 의해 형성된다.
이 부분을 엄밀히 하려면 컵에서 컵 아닌 것을 완벽하게 배제해야 한다. 이렇게 계속 배제하다 보면 컵은 사라져버린다. 이를 막으려면 컵의 정의는 컵이 아니라 컵을 쥐려는 사람에 의해 결정됨을 알 수 있다.
사람과 컵 사이의 일대일 대응이 칸토어의 1인 것이다. 그렇다면 컵이 아닌 사람을 보아야 컵을 찾을 수 있다. 사람은 어디까지 사람인가? 일단 사람의 손이 컵을 잡지만 실제로는 뇌가 컵을 잡는 것이다. 손은 도구에 불과하다.
사람은 칼손잡이를 잡지만 실제로는 칼날을 쓴다. 이렇듯 잡다한 것을 완벽하게 배제하면 뇌 안의 한 점만 남는다. 뇌 안의 한 점에 대응하는 컵의 한 점은 무게중심이다. 뇌 안의 한 점과 컵의 무게중심의 일대일 대응이 1이다.
그 뇌세포 하나와 컵의 무게중심 사이의 모든 것은 소거되어야 한다. 이때 그 중간을 완벽하게 소거했을 때 최종으로 남는 것은? 입체다. 즉 입체란 어떤 둘의 일대일 정면대응인 것이다.
우리는 입체를 덩어리라고 생각하지만 구조론적 입체는 어떤 둘의 충돌순간의 전자기력의 상호작용 모습이다. 우주의 한 지점에서 어떤 둘을 충돌시켰을 때 광속을 넘지 못하면서 투입된 에너지가 질량으로 변하는 모습이 4차원이다. 거기서 에너지를 배제한 모습이 3차원이다. 둘의 충돌이 아니라 일방의 충돌은 각이다. 그 충돌하는 진행은 선이다. 그 충돌하는 포지션은 점이다.
입체는 일대일 대응이며 각, 선, 점 일대일 대응에도 미치지 못한다. 각은 대응하러 가다가 꺾이는 것이며, 선은 대응하려고 연결하는 것이며, 점은 대응하려고 자기 포지션을 찾는 것이다.
점으로 포지션을 정하고, 선으로 잇고, 각으로 꺾어서, 입체로 대응하고, 에너지를 전달하면 밀도이며, 즉 공간의 차원이란 A와 B사이에 어떻게 에너지를 전달할 것인가를 결정하는 문제인 것이다.
그 핵심은 일대일 대응이고 구조론에서는 이를 상호작용이라 한다. 구조론은 상호작용 하나로 모든 것을 설명한다. 이 역시 언어의 문제다. 어떤 기자가 신문기사를 다음과 같이 썼다고 치자.
“윤석민 선수 직구를 던졌습니다. 박병호 선수 방망이를 휘둘렀습니다. 윤석민 선수가 던진 공의 전자기력이 박병호 선수가 휘두른 방망이의 전자기력과 마주쳐서 서로 밀어내는 반발력을 일으켜서 홈런이 되었습니다.”
그 기자는 짤렸다. 언어의 문제다. 언어를 받아들일 배짱이 있는가이다.
◎ 의미를 버리고 맥락을 취할 배짱이 있는가?
◎ 이태리 가구를 버리고 핀란드 가구를 취할 배짱이 있는가?
◎ 아카데미즘을 버리고 인상주의를 취할 배짱이 있는가?
◎ 극화를 버리고 병맛을 취할 배짱이 있는가?
◎ 텍스트를 버리고 이미지를 취할 배짱이 있는가?
◎ 뽕짝을 버리고 K팝을 취할 배짱이 있는가?
‘노인을 위한 나라는 없다’를 보고 그 영화의 줄거리가 아니라 그 영화의 느낌과 같은 섬뜩한 느낌을 주는 일상의 섬뜩한 체험을 이야기할만한 충분한 체험을 그대는 수집해 두고 있는가? 인생을 180도로 트는 문제이다. 그것을 틀지 못해서 크로네커는 칸토어를 죽였다.